Trong bài này ta chỉ định nghĩa hàm Lambert W biến số thực và ứng dụng của nó trong việc biểu diễn nghiệm của một số phương trình mũ (không...
Trong bài này ta chỉ định nghĩa hàm Lambert W biến số thực và ứng dụng của nó trong việc biểu diễn nghiệm của một số phương trình mũ (không biểu diễn được dưới dạng 'sơ cấp').
1. Sơ lược về hàm Lambert W
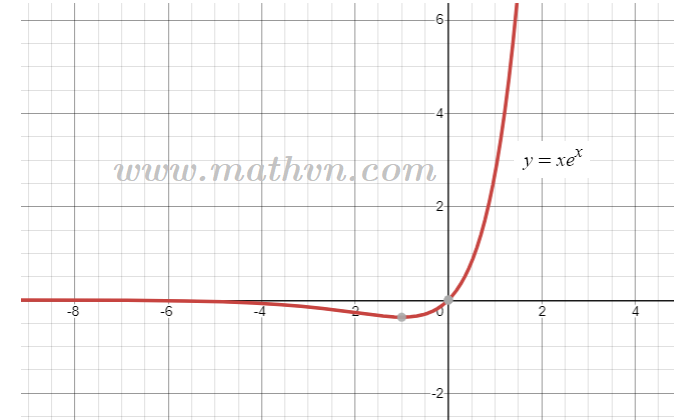
Xét hàm số biến số thực:
$$f(x)=xe^x$$
Hàm số này có miền xác định $\mathbb{R}$ (nhưng dưới đây ta chỉ xét trên một nửa khoảng thích hợp) và có miền giá trị $T=[-\frac{1}{e}; +\infty).$
Hàm $f$ đồng biến trên nửa khoảng $[-1;+\infty)=D$ nên $f$ có hàm ngược $f^{-1}$
- với tập xác định là $D_1=T=[-\frac{1}{e}; +\infty)$
- và tập giá trị là $T_1=D=[-1;+\infty)$
Hàm ngược này được gọi là hàm Lambert W (các tên gọi khác: hàm omega, hàm tích log (product log), hàm W), kí hiệu $W$.
Vậy $$W(x)=f^{-1}(x), \forall x \ge -\frac{1}{e}.$$
2. Tính chất hàm Lambert W
Từ tính chất của hàm ngược ta có:
1) $W(xe^x)=W(f(x))=f^{-1}(f(x))=x.$
2) $W(x)e^{W(x)}=f(W(x))=x.$
Tính chất 1) sẽ được dùng trong các ví dụ dưới đây.
3. Ứng dụng hàm Lambert W để biểu diễn nghiệm
Ví dụ 1. Giải phương trình sau: $x^x=2. \ \ \ (*) $
Một phương trình nhìn rất đơn giản nhưng để giải nó bằng các phương pháp sơ cấp thì không dễ tí nào. Bây giờ ta sẽ dùng hàm Lambert W để biểu diễn nghiệm của nó.
Với điều kiện $x > 0,$ phương trình $(*)$ tương đương với
$\ln x^x = \ln 2 \Leftrightarrow x\ln x = \ln 2 \Leftrightarrow e^{\ln x}\ln x = \ln 2$
$\Leftrightarrow W(\ln x . e^{\ln x}) = W(\ln 2) \Leftrightarrow \ln x = W(\ln 2) $
$\Leftrightarrow x = e^{W(\ln 2)}.$
Vậy nghiệm của phương trình $(*)$ là: $x = e^{W(\ln 2)}$
Nghiệm này có giá trị xấp xỉ $1.559610469462369349970388768765002993284883511843091424719...$
Ví dụ 2. Giải phương trình sau: $x^2=2^x. \ \ \ (**) $
Bằng phương pháp tương tự ví dụ 1 ta tìm được 3 nghiệm của phương trình $(**)$ là
$$x=2, \ x=4, \ x=-e^{-W(\ln \sqrt{2})}.$$
Nghiệm thứ ba có giá trị xấp xỉ là $-0.766664695962123093111204422510314848006675346669832058460...$
Người đăng: Sơn Phan.