Bài toán parabol tiếp xúc với hai đường tròn bằng nhau là một bài toán đẹp. Lời giải sử dụng cả hình học và giải tích để giải quyết. Đề bà...
Bài toán parabol tiếp xúc với hai đường tròn bằng nhau là một bài toán đẹp. Lời giải sử dụng cả hình học và giải tích để giải quyết.
Do $R$ là trung điểm của đoạn $MN$ nên $R(\frac{n}{2};\frac{m}{2}).$
Vì $R$ thuộc parabol nên $\frac{m}{2}=(\frac{n}{2})^2.$
Làm gọn ta được phương trình: $2m=n^2.$
Ngoài ra, tiếp tuyến của parabol tại $R$ có hệ số góc là $y'(\frac{n}{2})=2.\frac{n}{2}=n.$
Còn hệ số góc của đường thẳng $MN$ là $-\frac{m}{n}.$
Tiếp tuyến này vuông góc với $MN$ nên ta có: $-\frac{m}{n}.n=-1.$
Làm gọn ta được: $m=1.$
Thay vào phương trình ở trên ta được $n=\sqrt{2}.$
Vậy bán kính đường tròn là $r=\frac{MN}{2}=\frac{\sqrt{3}}{2}.$
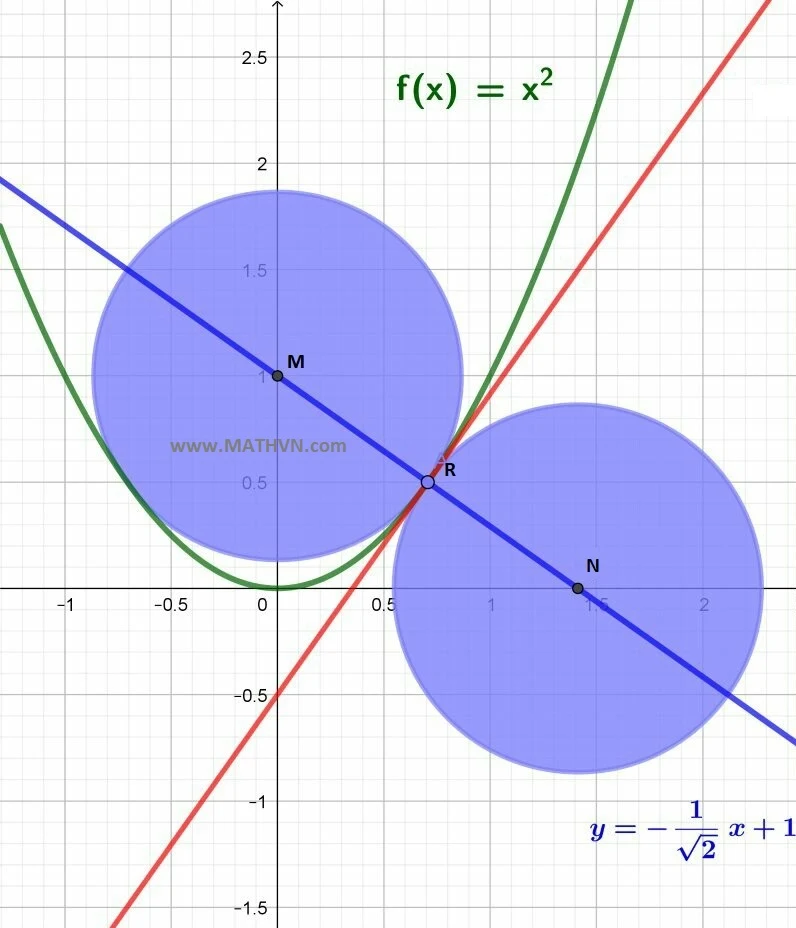
Đề bài toán parabol và 2 đường tròn
Hai đường tròn bằng nhau, tiếp xúc với parabol $y=x^2 \ \ \ $ cùng tại một điểm $R$ như hình vẽ. Tính bán kính $r$ của đường tròn.Lời giải bài toán parabol và 2 đường tròn
Gọi $M(0;m)$ và $N(n;0).$Do $R$ là trung điểm của đoạn $MN$ nên $R(\frac{n}{2};\frac{m}{2}).$
Vì $R$ thuộc parabol nên $\frac{m}{2}=(\frac{n}{2})^2.$
Làm gọn ta được phương trình: $2m=n^2.$
Ngoài ra, tiếp tuyến của parabol tại $R$ có hệ số góc là $y'(\frac{n}{2})=2.\frac{n}{2}=n.$
Còn hệ số góc của đường thẳng $MN$ là $-\frac{m}{n}.$
Tiếp tuyến này vuông góc với $MN$ nên ta có: $-\frac{m}{n}.n=-1.$
Làm gọn ta được: $m=1.$
Thay vào phương trình ở trên ta được $n=\sqrt{2}.$
Vậy bán kính đường tròn là $r=\frac{MN}{2}=\frac{\sqrt{3}}{2}.$
Người đăng: Sơn Phan.