Bài này sẽ tổng hợp một số kiến thức liên quan đến hình thang cân và hình thang nội tiếp đường tròn . 1. Hình thang cân là gì? a. Định ng...
Bài này sẽ tổng hợp một số kiến thức liên quan đến hình thang cân và hình thang nội tiếp đường tròn.
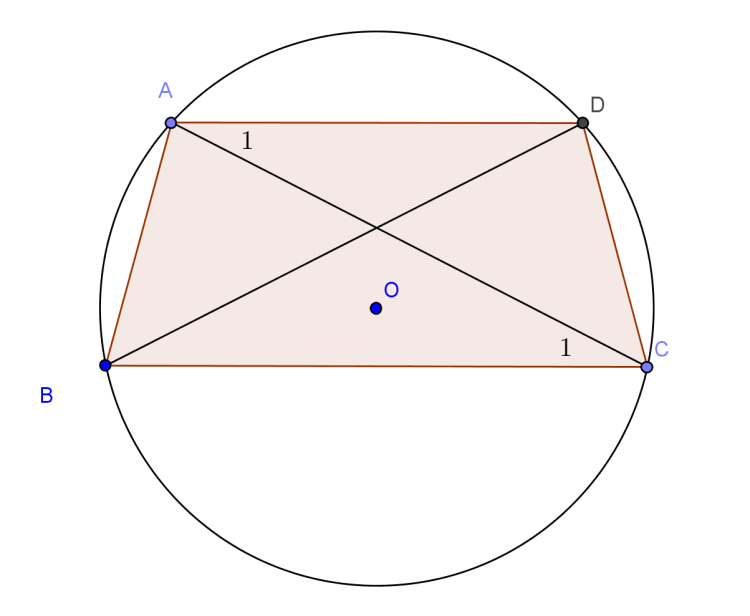
Phản ví dụ đơn giản nhất chính là hình bình hành (như trong ảnh trên).
Chứng minh bài toán này dành cho độc giả.
1. Hình thang cân là gì?
a. Định nghĩa hình thang cân
(Trong hình học Euclid), hình thang cân là hình thang có hai góc kề một cạnh đáy bằng nhau. |
| Hình thang cân ABCD với trục đối xứng d |
b. Tính chất của hình thang cân
Dễ dàng chứng minh được hình thang cân có các tính chất sau:- Hai cạnh bên bằng nhau.
- Hai góc kề cạnh đáy bằng nhau.
- Hai đường chéo bằng nhau.
- Hình thang cân nội tiếp được trong một đường tròn. (Hình thang cân luôn có đường tròn ngoại tiếp).
2. Hình thang có 2 cạnh bên bằng nhau
Trong tính chất 1 ở trên, ta thấy hình thang cân có 2 cạnh bên bằng nhau. Tuy nhiên điều ngược lại không đúng, tức: hình thang có 2 cạnh bên bằng nhau có thể không phải là hình thang cân. |
| Hình bình hành trong ảnh là một "hình thang có 2 cạnh bên bằng nhau" nhưng không phải là "hình thang cân". |
3. Hình thang nội tiếp đường tròn
Tính chất 4 ở trên nói rằng "hình thang cân luôn nội tiếp được trong một đường tròn". Và chiều ngược lại cũng đúng, tức: một hình thang nội tiếp đường tròn là hình thang cân.Chứng minh bài toán này dành cho độc giả.
Tổng hợp: Tố Uyên Trần.