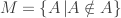Nghịch lý Russell (Russell’s paradox) được mô tả qua một câu chuyện vui về ông thợ cạo như sau: Ngày xưa, có 1 ông thợ cạo, sống ở làng Sev...
Nghịch lý Russell (Russell’s paradox) được mô tả qua một câu chuyện vui về ông thợ cạo như sau:
Nếu thuộc nhóm tự cạo râu (nhóm 1) thì ông không cạo cho những người tự cạo râu, tức là ông không cạo cho ông. Nhưng nếu như vậy thì ông phải thuộc nhóm không tự cạo râu (nhóm 2).
Nếu ở nhóm 2 thì ông sẽ cạo râu cho ông vì ông cạo râu cho những người thuộc nhóm 2. Lúc đó hoá ra ông lại tự cao râu cho mình. Hóa ra, ông là người thuộc nhóm 1.
Vậy thì ông thợ cạo sẽ như thế nào?
Điều trên có lẽ chỉ xảy ra nếu như người thợ cạo đó không sống ở làng Seville. Đây là điều không thể, vì ở đầu câu truyện đã nói rõ, người thợ cạo có lẽ sống ở làng Seville. Vậy thì người thợ cạo chỉ có thể là phụ nữ !!! Lại không đúng nốt. Vì trong câu chuyện đã nói rõ có 1 ông thợ cạo.
Vậy mâu thuẫn ở đây là gì? Hay đây là câu chuyện không có thật. Nghĩa là Russell đã nói dối. Có lẽ, không phải vậy, bởi nếu thế, ông đã không thể trở thành nhà toán học lỗi lạc, và câu chuyện trên sẽ phải bị xếp xó chứ không trở thành nghịch lý Russell nổi tiếng ngày nay.
Thật ra, câu chuyện này dùng để minh họa cho 1 loại mâu thuẫn gặp phải trong lý thuyết tập hợp. Khi ta xét tập hợp :”S là tập hợp của tất cả các tập hợp” để rồi gặp phải tình huống: “Một phần tử thuộc hoặc không thuộc tập S đều dẫn đến mâu thuẫn”. Sau đó, để tránh sai lầm trên, người ta không dùng thuật ngữ “tập hợp của tất cả các tập hợp” mà đề xuất một khái niệm mới, tổng quát hơn là “lớp”. Trong đó, người ta chỉ cần khoanh vùng một tập hợp bao gồm đủ nhiều các tập hợp nào đó (nhưng không phải là tất cả) để làm việc thì sẽ không phải gặp mâu thuẫn nữa.
Một phần của nghịch lý, được khám phá bởi Bertrand Russell vào năm 1901.
Giả sử tập M là “tập hợp tất cả các tập hợp không chứa chính nó”. Một cách hình thức : A là một phần tử của tập M nếu và chỉ nếu A không là phần tử của chính A.
Ngày xưa, có 1 ông thợ cạo, sống ở làng Seville. Tại làng đó, tất cả đàn ông đều tự cạo râu hoặc nhờ thợ cạo. Và ông thợ này đã tuyên bố: “Tôi chỉ cạo râu cho những người đàn ông nào của làng Seville mà không tự cạo râu”.Đây là câu chuyện rất thú vị được kể nguyên văn từ nhà toán học Bertrand Russell nhưng cũng đầy rắc rối. Rắc rối vì, nếu như thế các đấng nam nhi của làng chia làm 2 nhóm: nhóm tự cạo râu và nhóm không tự cạo râu. Vậy thì thợ cạo thuộc nhóm nào đây?
Nếu thuộc nhóm tự cạo râu (nhóm 1) thì ông không cạo cho những người tự cạo râu, tức là ông không cạo cho ông. Nhưng nếu như vậy thì ông phải thuộc nhóm không tự cạo râu (nhóm 2).
Nếu ở nhóm 2 thì ông sẽ cạo râu cho ông vì ông cạo râu cho những người thuộc nhóm 2. Lúc đó hoá ra ông lại tự cao râu cho mình. Hóa ra, ông là người thuộc nhóm 1.
Vậy thì ông thợ cạo sẽ như thế nào?
Điều trên có lẽ chỉ xảy ra nếu như người thợ cạo đó không sống ở làng Seville. Đây là điều không thể, vì ở đầu câu truyện đã nói rõ, người thợ cạo có lẽ sống ở làng Seville. Vậy thì người thợ cạo chỉ có thể là phụ nữ !!! Lại không đúng nốt. Vì trong câu chuyện đã nói rõ có 1 ông thợ cạo.
Vậy mâu thuẫn ở đây là gì? Hay đây là câu chuyện không có thật. Nghĩa là Russell đã nói dối. Có lẽ, không phải vậy, bởi nếu thế, ông đã không thể trở thành nhà toán học lỗi lạc, và câu chuyện trên sẽ phải bị xếp xó chứ không trở thành nghịch lý Russell nổi tiếng ngày nay.
Thật ra, câu chuyện này dùng để minh họa cho 1 loại mâu thuẫn gặp phải trong lý thuyết tập hợp. Khi ta xét tập hợp :”S là tập hợp của tất cả các tập hợp” để rồi gặp phải tình huống: “Một phần tử thuộc hoặc không thuộc tập S đều dẫn đến mâu thuẫn”. Sau đó, để tránh sai lầm trên, người ta không dùng thuật ngữ “tập hợp của tất cả các tập hợp” mà đề xuất một khái niệm mới, tổng quát hơn là “lớp”. Trong đó, người ta chỉ cần khoanh vùng một tập hợp bao gồm đủ nhiều các tập hợp nào đó (nhưng không phải là tất cả) để làm việc thì sẽ không phải gặp mâu thuẫn nữa.
Một phần của nghịch lý, được khám phá bởi Bertrand Russell vào năm 1901.
Giả sử tập M là “tập hợp tất cả các tập hợp không chứa chính nó”. Một cách hình thức : A là một phần tử của tập M nếu và chỉ nếu A không là phần tử của chính A.
Nếu M chứa chính nó thì theo định nghĩa của M, tập M không phải là một phần tử của M . Nếu M không chứa chính nó thì cũng do định nghĩa của M chính M lại là một phần tử của M. Các mệnh đề “M là một phần tử của M” và “M không là phần tử của M” cả hai không thể đúng, đó chính là mâu thuẫn.
Nghịch lý này thúc đẩy Russell phát triển lý thuyết kiểu và Ernst Zermelo phát triển lý thuyết tập hợp tiên đề ngày nay trở thành lý thuyết tập hợp Zermelo-Fraenkel.
